Efficient components and systems for heating technology

To date we are the only company in the world to develop blowers, venturis, valves and combustion controllers together with our customers and supply everything as a full package.
Everyone who has ever started up a grill knows that without enough air the flame quickly goes out. The same thing happens in a gas condensing unit. If not enough air is available, the gas does not combust completely, and soot and carbon monoxide are generated.
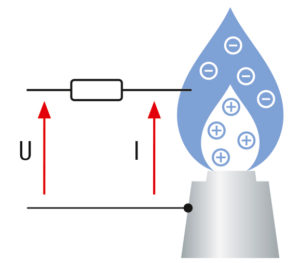
In gas condensing units, a system comprising venturi, combustion air blower, and gas valve has proven successful for mixture control — so-called pneumatic gas/air ratio control: depending on the amount of air conveyed, suction pressure arises in a venturi, which adds the applicable amount of gas from the gas control valve.
The control shows its limits, however, when the suppliers must flexibly feed new gas sources and alternative fuel into the networks. Gas-adaptive systems that automatically adjust to the fuel are therefore essential. But they can only function with an electronic gas/air ratio control. It doesn’t need a venturi, which produces pressure loss, since the gas is only supplied by actuating an electronically controlled gas valve.
This is possible because in an electronic gas/air ratio control, the control of the gas-air mixture only depends on the combustion product: the flame.

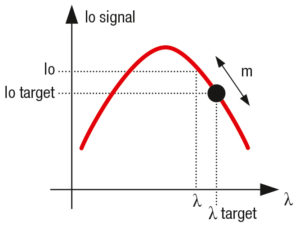
Background information: Combustion is a chemical reaction that sets electrons free. This means the flame can conduct electricity. If voltage is applied externally, a small electric current called “ionization current” flows through the flame. When the current has achieved its maximum, combustion is perfect, and the λ-value is 1.
However, the maximum value should not be achieved. As in the case of a pneumatic gas/air ratio control, a safety buffer is included in the calculation. For example, the target λ value is 1.3, an area in which the relationship between the ionization current and the λ value is virtually linear.
The combustion mixture control depends solely on the ionization current. The formula shows how simple the relationship is: If the ionization current is too small, more gas is fed in. If it is too high, the gas supply is restricted.

Leave a comment