Everyone who has ever started up a grill knows that without enough air the flame quickly goes out. The same thing happens in a gas condensing unit. If not enough air is avail­able, the gas does not combust completely, and soot and carbon monoxide are gener­ated.

Hartmut Henrich, Product Manage­ment Combus­tion Systems in Osnabrück (Photo | ebm-papst)

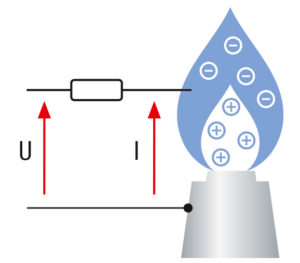
Elec­trons are set free during combus­tion. When a voltage U is applied, a small elec­tric current I, called an “ioniza­tion current,” flows through the flame.

In gas condensing units, a system comprising venturi, combus­tion air blower, and gas valve has proven successful for mixture control — so-called pneu­matic gas/air ratio control: depending on the amount of air conveyed, suction pres­sure arises in a venturi, which adds the applic­able amount of gas from the gas control valve.

The control shows its limits, however, when the suppliers must flex­ibly feed new gas sources and alter­na­tive fuel into the networks. Gas-adap­tive systems that auto­mat­i­cally adjust to the fuel are there­fore essen­tial. But they can only func­tion with an elec­tronic gas/air ratio control. It doesn’t need a venturi, which produces pres­sure loss, since the gas is only supplied by actu­ating an elec­tron­i­cally controlled gas valve.

This is possible because in an elec­tronic gas/air ratio control, the control of the gas-air mixture only depends on the combus­tion product: the flame.

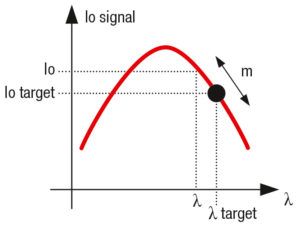
The rela­tion­ship between the ioniza­tion current and the λ-value is prac­ti­cally linear. This makes control in an elec­tronic gas/air ratio control less complex.

Back­ground infor­ma­tion: Combus­tion is a chem­ical reac­tion that sets elec­trons free. This means the flame can conduct elec­tricity. If voltage is applied exter­nally, a small elec­tric current called “ioniza­tion current” flows through the flame. When the current has achieved its maximum, combus­tion is perfect, and the λ-value is 1.

However, the maximum value should not be achieved. As in the case of a pneu­matic gas/air ratio control, a safety buffer is included in the calcu­la­tion. For example, the target λ value is 1.3, an area in which the rela­tion­ship between the ioniza­tion current and the λ value is virtu­ally linear.

The combus­tion mixture control depends solely on the ioniza­tion current. The formula shows how simple the rela­tion­ship is: If the ioniza­tion current is too small, more gas is fed in. If it is too high, the gas supply is restricted.